Histograma (para datos no agrupados)
Amplitud = Rango/k
Rango = Valor máximo - Valor mínimo
K = Número de clases
N = Número de datos totales
Número de clases = RAIZ(N)
Polígono de frecuencias
Marca de clase = (Limite superior + Limite inferior)/2
Media
Media aritmética (datos no agrupados)
La media aritmética es el valor obtenido al sumar todos los
datos y dividir el resultado entre el número total de datos
Donde N= es igual al número de datos totales.
Media aritmética datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias,
la expresión de la media es:
Ejemplo:
En test realizado a un grupo de personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuacion media:
En test realizado a un grupo de personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuacion media:
Observaciones sobre la media
aritmética
1.
La media se puede hallar solo para variables
cuantitativas.
2.
La media es independiente de las amplitudes de
los intervalos
3.
3.- La media es muy sensible a las puntuaciones
extremas. Si tenemos una distribución con los siguientes pesos:
65 kg. 69 kg. 65 kg. 72 kg. 66kg. 75kg. 110kg.
La media es igual a 74 kg. Que es una medida de centralización poco representativa de la distribución.
65 kg. 69 kg. 65 kg. 72 kg. 66kg. 75kg. 110kg.
La media es igual a 74 kg. Que es una medida de centralización poco representativa de la distribución.
4.
La media no se puede calcular si hay un
intervalo con amplitud indeterminada.
Mediana
Es el valor que ocupa el lugar central de todos los datos
cuando estos están ordenados de menor a mayor.
La mediana se representa por Me
La mediana solo se puede hallar solo para variables cuantitativas.
La mediana se representa por Me
La mediana solo se puede hallar solo para variables cuantitativas.
Mediana Para datos no agrupados:
1.
Ordenamos los datos de menor a mayor.
2.
SSi la serie tiene un número impar de medidas la
mediana es la puntuación central de la misma.
3.
Si la serie tiene un número par de las
puntuaciones la media es la media entre las dos puntuaciones centrales.
Calculo de mediana para datos agrupados.
La mediana se encuentra en el intervalo donde la frecuencia
acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se
encuentre, con la siguiente formula.
Li -1: Es
el límite inferior de la clase donde se encuentra la mediana
Fi – 1 es la frecuencia acumulada anterior a la clase
mediana
a_i =
a la amplitud de la clase
La mediana es independiente de las amplitudes de los intervalos.
Ejemplo
Calcular la mediana de una distribución estadística que vienen dada por la siguiente tabla
Calcular la mediana de una distribución estadística que vienen dada por la siguiente tabla
100/2 = 50:.
Clase modal: [66, 69)
Moda.
Moda para datos no agrupados
La moda es el valor que tiene mayor frecuencia absoluta.
Se representa por Mo.
Se representa por Mo.
Se puede hallar la moda para variables cualitativas y
cuantitativas
Hallar la moda de la siguiente distribución
Si en un grupo hay dos o varias puntuaciones (modas) con la misma
frecuencia y esa frecuencia es la máxima, la distribución es bimodal o
multimodal, es decir, tiene varias modas.
Cuando todas las puntuaciones de un grupo tienen la misma
frecuencia, no hay moda.
Si dos puntaciones adyacentes tienen la misma frecuencia
máxima, la moda es el promedio de las dos puntuaciones adyacentes
Calculo de moda para datos no agrupados
1.- Todos los intervalos tienen la misma
amplitud
También se utiliza otra fórmula de la moda que da un valor
aproximado de esta
Ejemplo
Calcular la moda de una distribución estadística que viene
dada por la siguiente tabla
2.- Los intervalos tienen amplitudes distintas.
En primer lugar tenemos que hallar las alturas.
La clase modal es la que tiene mayor altura
La fórmula de la moda aproximada cuando existen distintas
amplitudes es:










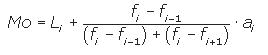







No hay comentarios:
Publicar un comentario